How To Classify Real Numbers

The Real Number System

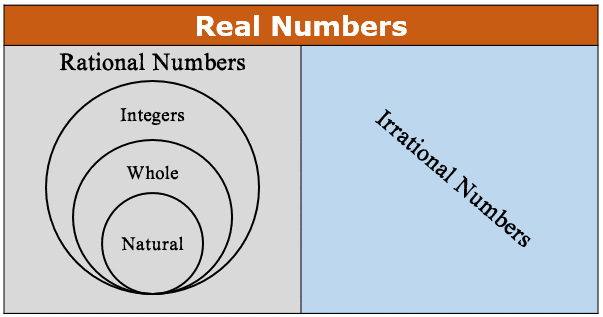
All the numbers mentioned in this lesson belong to the set of Real numbers. The set of real numbers is denoted by the symbol $\mathbb{R}$ . In that location are 5 subsets within the ready of real numbers. Let'south get over each one of them.

V (5) Subsets of Real Numbers

ane) The Fix of Natural or Counting Numbers

The set of the natural numbers (besides known every bit counting numbers) contains the elements

the symbol of the set of natural numbers is N. moreover, the elements of the set of natural numbers can be expressed as {1,2,3,4,5,6,...}.

The ellipsis "…" signifies that the numbers proceed forever in that pattern.

2) The Ready of Whole Numbers

The set up of whole numbers includes all the elements of the natural numbers plus the number goose egg (0).

the symbol W indicates the set of whole numbers. on the other hand, the elements of the set of whole numbers can be expressed as {0, 1, 2, 3, 4, 5, 6, ...}.

The slight addition of the element zero to the set of natural numbers generates the new set of whole numbers. Elementary as that!

3) The Set of Integers

The set of integers includes all the elements of the set of whole numbers and the opposites or "negatives" of all the elements of the set of counting numbers.

the symbol for the set of integers is Z while the elements of the set of integers can be expressed as {-4, -3, -2, -1, 0, 1, 2, 3, 4, ...}.

4) The Prepare of Rational Numbers

The set of rational numbers includes all numbers that tin can be written every bit a fraction or as a ratio of integers. However, the denominator cannot exist equal to naught.

the symbol Q indicates the set of rational numbers. meanwhile, the elements of the set of rational numbers are expressed as a/b where a and b are integers but b≠0.

A rational number may also appear in the form of a decimal. If a decimal number is repeating or terminating, it can be written as a fraction, therefore, information technology must exist a rational number.

Examples of terminating decimals:

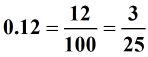
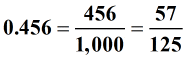
Examples of repeating decimals:

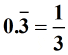
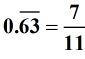
5) The Set of Irrational Numbers

The gear up of irrational numbers can be described in many ways. These are the common ones.

Irrational numbers are numbers that cannot be written as a ratio of ii integers. This clarification is exactly the opposite of that of rational numbers.

Irrational numbers are the leftover numbers after all rational numbers are removed from the set of the real numbers. You may remember of information technology as,

irrational numbers = real numbers "minus" rational numbers

Irrational numbers if written in decimal forms don't terminate and don't repeat.

There's really no standard symbol to represent the prepare of irrational numbers. But you may encounter the one beneath.

the symbol for the set of irrational numbers is RQ while the elements of the set of rational numbers can be expressed as real numbers "minus" rational numbers.

Examples:

a) Pi

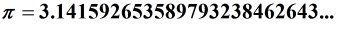
b) Euler's number

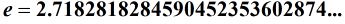
c) The foursquare root of ii

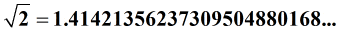
Here'due south a quick diagram that can help yous allocate existent numbers.

a diagram of the real number system showing real numbers classified into two sets, namely, the sets of rational and irrational numbers. within the set of rational numbers are the set of natural or counting numbers, the set of whole numbers, and the set of integers.

Practice Problems on How to Classify Real Numbers

Example 1: Tell if the statement is true or simulated. Every whole number is a natural number.

Solution: The set of whole numbers includes all natural or counting numbers and the number zilch (0). Since zero is a whole number that is NOT a natural number, therefore the statement is FALSE.

Instance 2: Tell if the statement is truthful or false. All integers are whole numbers.

Solution: The number -ane is an integer that is Non a whole number. This makes the statement FALSE.

Example iii: Tell if the argument is true or false. The number zero (0) is a rational number.

Solution: The number zippo tin exist written equally a ratio of two integers, thus it is indeed a rational number. This argument is TRUE.

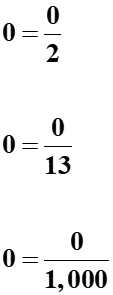
Example four: Proper name the set up or sets of numbers to which each real number belongs.

1) $7$

It belongs to the sets of natural numbers, {1, 2, 3, iv, 5, …}. It is a whole number because the set of whole numbers includes the natural numbers plus goose egg. It is an integer since it is both a natural and a whole number. Finally, since 7 tin be written as a fraction with a denominator of 1, 7/1, then information technology is also a rational number.

two) $0$

This is not a natural number because information technology cannot be found in the prepare {1, ii, 3, 4, v, …}. This is definitely a whole number, an integer, and a rational number. It is rational since 0 can be expressed as fractions such as 0/iii, 0/16, and 0/45.

three) $0.3\overline {xviii}$

This number obviously doesn't belong to the ready of natural numbers, ready of whole numbers, and set of integers. Discover that eighteen is repeating, and so this is a rational number. In fact, we can write it as a ratio of two integers.

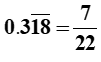
4) $\sqrt 5$

This is non a rational number because it is not possible to write it as a fraction. If we evaluate it, the square root of 5 will have a decimal value that is non-terminating and non-repeating. This makes it an irrational number.